John Nash and Game Theory

John Nash. A name nearly everyone would have heard. But what exactly did he do? Possibly, many people know that he came up with a concept of equilibrium known as the “Nash Equilibrium”.

What is a game?

A game basically consists of the following things –

1. Players — Duh! If you have a game you ought to have players, right?
2. Actions — Again, obvious. Every player has a bunch of things (s)he can do.
3. Payoffs — What would they play for if there is no money to be made? So, we specify how much does each player get, given all the actions chosen by players.

Nearly every interaction around us can be modeled as a game, at least every interaction of interest. Think about two firms competing in a market, an auction. Game theory is about formulating various strategic interactions between individuals in a systematic form through the three things I have mentioned and then thinking about the possible outcomes. Economics, by and large, is of interest to people and policymakers only if it has some explanatory power. Once we model interactions of interest as a ‘game’ then we proceed to predict as to what might happen.

To illustrate, the example of the famous prisoner’s dilemma should help. This is the most popular game in the economics literature and numerous papers have been written on this single game. They study this game in depth because countless interactions can be modeled and studied through this game.

Consider two prisoners charged with theft. They are locked up and are going to be interrogated separately. At the end of their interrogation, if both of them confess to having stolen, they will be jailed for 6 months. Let’s say that gets them a payoff of ‘0’ each. If one person confesses and the other denies then the one denying gets an extra penalty for lying and is locked up for a year giving him, say, ‘- 5’. One confessing is rewarded for his co-operation and is let go in ten days earning him, say, + 10.  If both deny then they are acquitted in a month giving a payoff of, say, + 5 each. This is what it looks like in a table.

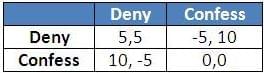
Column 1 represents Player 1’s actions and row 1 is Player 2’s actions. They payoff is written as player 1’s payoff followed by Player 2’s. For example, if P1 plays Confess and P2 plays Deny then we look at the bottom row and first column (in the payoffs) to get (10, -5). That is, P1 makes 10 and P2 makes – 5.

Let’s think about what might happen in this game. They would both undoubtedly prefer both denying over both confessing. But, if say P1 is certain that P2 is denying then P1 can simply cheat and confess to get 10. And P2 would be aware that P1 could do such a thing and therefore will not want to play Deny. If he is certain that P1 won’t cheat even then he might as well confess and make 10 rather than going for deny. The end result is they will both play ‘confess’. Observe why I am saying they will both confess. The reason is that, given P2 is confessing, P1 finds it optimal to confess. Similarly, given that P1 is confessing, P2 finds it optimal to confess.

We arrived at this reason without players having to communicate with each other. Just the fact that they both know that they are rational (to be elaborated upon in some future post) they will play deny. Notice that if they could write a contract they would happily do so to ensure both of them deny. But the problem is they can’t. That’s what real-life situations are about more often than not.

Here comes the concept of Nash equilibrium (NE). NE is a concept of what will happen in a game. It is not a normative concept i.e. we do not desire that people always play NE. It is how they will play. Basically NE is an action specified for each player. For example, in prisoner’s dilemma it was (Confess, Confess) such that every player reasons the following way:

He looks at his action and looks at other players’ action. Thinks in his head can he do better by playing something else other than the action specified? If the answer is no then he sticks to his specified action.

Every player does this in their head if the answer is “no” for every player, i.e. given everybody else’s specified action, every player finds it optimal to play what they are prescribed then this action profile is a Nash Equilibrium. A casual google/ Wikipedia link will give abundant links on this topic. Observe that our (Confess, Confess) is a Nash Equilibrium for exactly this reason. Given one person is confessing the other finds it best to confess and vice versa.

Obviously, there are natural questions if we like this idea of equilibrium. Now, we have a well-specified object to think of what might happen in a game. It doesn’t seem vacuous in the sense that we seem to be able to say something precise regarding the outcome of the game. The question then is, does every game have such an equilibrium? It sounds too restrictive right? The requirement is that everyone is happy playing a certain action given the other players’ actions and this happens for all the players. How do we know that such a thing might happen in any game?

John Nash, a graduate student in mathematics at Princeton first submitted his short paper to the National Academy of Sciences in 1950 and then went on to publish his thesis in the Annals of Mathematics, the most prestigious journals in mathematics. He showed that in any such game there will always exist a Nash Equilibrium provided certain simple conditions are satisfied. Now, here is a concept that seems intuitively appealing and can work in every game! That is a powerful tool for anyone who wishes to study any strategic interaction in any context.

This is why economists caught on to this concept and applied it in broad settings to study various institutions. For example, in the prisoner’s dilemma it might be beneficial to have both the players play Deny. But we now know that cannot happen. In various complex settings therefore we have a machine that tells us what can possibly happen in a game. Now we can compare this against what is desirable to see if our institution will perform well or not.

The history of game theory before Nash and how he transformed the entire field of economics is too big to be written about in this article. In the times before Nash, starting from a French economist Antoine Augustin Cournot who was interested in studying oligopoly to von Neumann, to whom we owe the formulation of games as we know today, a number of extraordinary minds tried to answer some questions in game theory, a field that wasn’t even born then.

But it took the extraordinary genius of Nash to unify them all, to highlight where each of the models stands and to give a framework for the rest of the field to address questions for the decades to come. There is a fantastic essay on Nash Equilibrium by Roger Myerson, one of my favourite economists about whom I will write at some point, that tells the historical context of Nash Equilibrium and why and how it transformed the field. When one talks about some of the greatest successes and insights of economics people talk about auction theory and information economics, neither of which would be possible had Nash not unified it all for us. As Myerson says in his essay,

“Thus, by accepting noncooperative game theory as a core analytical methodology alongside price theory, economic analysis has returned to the breadth of vision that characterized the ancient Greek social philosophers who gave economics its name.”

And if that doesn’t humble you yet, Nash’s best work is not considered to be this. It is in another extremely deep field in mathematics. This, if anything, was just the beginning. To attempt unification of theories given by the legends like von-Neumann, as a graduate student is audacity. To do it so well is genius. For that alone we should be grateful to one of the greatest minds alive today.