What’s In A Number? What If We Say, Names, And Vedic Knowledge

A joke doing the rounds on WhatsApp goes thus: Aryabhata asked his wife what the chances were of his being allowed to stay out past midnight on New Year’s eve, and that’s when he discovered zero.

There is a double whammy of breathtaking ignorance in this joke. Aryabhata didn’t invent zero. The zero was in use in India, at least 700 years before Aryabhata. This is roughly like making a joke with a punchline involving Edison inventing the telescope.

The other irony is that Aryabhata was the first Indian astronomer to propose using midnight to mark the beginning of a day. Until then, sunrise marked the beginning of a day.

The WhatsApp joke is, therefore, historically flawed on two counts. Isn’t it ironic, that Indians don’t know what their most famous mathematician Aryabhata discovered?

Mathematicians Anonymous

In the Vedanga book on prosody Chanda Sutra, Pingala uses the word shunyam for zero. In the Vedanga book on grammar Ashtaadhyaayi, Panini uses the word lopaH, which some historians interpret as another word for zero. So strangely, it is not in the Jyotisha or Sulba Sutras, which deal with mathematics, but in the Vedanga books on language, that we first encounter the word.

Neither Panini nor Pingala claim to have discovered zero, or bother to explain the concept. They just assume that the reader understands.

So, the zero was quite well known by their era, estimated to be the second century BC or sixth century BC. Some anonymous mathematician gave us the zero.

We learn numerals, that is, the symbols 0,1,2,3 up to 9 and assume that that is always how numbers have been written. But the surviving literature shows us a slow evolution, with several gaps in the historical record.

We also assume that decimal numbering system (base 10) is normal, as the whole world uses it today, but as we will see, various civilisations developed different number bases and strikingly strange systems for notation of numerals.

Not only the zero, but also the place value system of decimal numbers is one of India’s greatest contributions to the mathematics of the world. Before diving into various of aspects of mathematics discovered and used in India, either by astronomers or others, it will be useful to understand how numbers were named and notated.

Numbers in Words

We can write any number, for example, 1729, in numerals; or in words as one thousand seven hundred and twenty-nine. Almost all literate societies developed words for large numbers.

Indians, perhaps, came up with the largest names and numbers. All Indian languages have adopted several hundreds, perhaps thousands of Sanskrit words; including words for numbers, sometimes in modified form.

Ek do teen, a song from the 1980s Hindi film Tezaab, perhaps taught more non-Hindi speaking Indians to count up to 13 than most government-funded schools.

Ek do teen and all Hindi number names (in fact, number names in the Indo-Aryan languages) come from the Sanskrit original Ekam, dvi, threeni, chatur, pancha, shad, sapta, ashta, nava and dasha. The southern Dravidian family of languages, though, use a different set of number names (one ancient distinction from the Aryan family).

The Tamil numbers from one to ten are onru, irandu, moonru, naangu, ainthu, aaru, ezhu, ettu, onpathu and patthu. Malayalam uses the same names, but Kannada, Tulu and Telugu use a set of words similar to Tamil, with common roots.

Names of higher numbers exhibit an interesting feature. In English, and other Indo-European languages, we write and say the most significant numeral first, and proceed in descending order to the least significant value: Thousands, hundreds, tens, ones. The Dravidian languages all follow this sequence, though unrelated to the Indo-European family.

So, 1729 is aayiraththu (thousand) ezhu (seven) nootru (hundred) irupatthu (twenty) onpathu (nine).

But Sanskrit number names go from least significant to most, in ascending order. Fourteen is chatur-dashi (four and ten); twenty-four is chatur-vimshati (four and twenty); and one thousand and eight is ashta-sahasram (eight and thousand).

Even as numeral notation, the notation was from least significant digit (LSD) to most significant digit (MSD). So, 1729 was written as 9271 (and would be called nava-vimshati sapta-shata sahasram).

We only find numbers written as words in ancient texts, not just Vedas and Vedangas, but also other literature, scientific or artistic. Numeral notation had as anonymous an inventor, as zero and the place value system (or any of the oldest concepts).

But remarkably, two other methods of expressing numbers in words were also developed.

BhutaSankhya भूतसङ्खया

Bhuta means body. Sankhya means number. In the BhutaSankhya system, instead of the familiar number names, the names of objects representing their values are used. The table below features, Numbers 0 through 9, their familiar number-names, the BhutaSankhya synonyms and the meanings of those words in English.

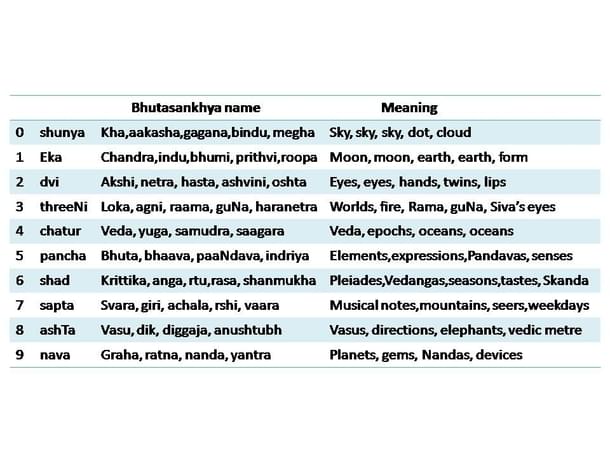
Using this system, the number 352 could be expressed as loka-paandava-netram or guna-bhuta-hasta. 1729 would be chandra-svara-ashvini-ratnam. They also would mix up the familiar number names with the Bhutasankyha synonyms.

For example, 5482 could be written as pancha-veda-ashta-netram. (For convenience of readability, I use the MSD to LSD order; in actual Sanskrit texts, it would be the reverse).

These BhutaSankhya phrases make no sense as grammatical or semantic constructs, but they have the advantage of being expressed in words.

As all our Sanskrit texts including siddhantas on astronomy and mathematics were composed in verse, they only have to fit the syllabic rules of chandas.

This also had the advantage of writing very large numbers without mentioning all the place names like.

For example, 1,44,63,895 could be written as eka-veda-veda-rasa-guna-vasu-ratna-paandava without all the mentions of crores, lakhs, thousands, hundreds etc. As compact as possible using words alone.

Obviously, some of the words are based on familiar physical objects. We have two eyes or lips, there is only one moon, eight directions, seven musical notes and nine precious stones, and so on.

Others are based on cultural artefacts of India — the three lokas, four vedas, seven rshis and mountains, six seasons (rtu), and even three Ramas (Parashu Rama, Rama of Ayodhya, Yadava Balarama) and the three eyes of Siva.

This is not confined to single digit numbers. Jina or arhat (for tirthankara) stands for 24, avatara or anguli stands for 10, nakshatra for 27, deva for 33 etc. So, the number 332724 may be written as deva-nakshatra-jina, wherein three words represent six digits.

Katapayaadi कटपयादि

The other system to represent numbers was using letters instead of words. The consonants (vyanjanaa) of the Sanskrit alphabet were arranged in the order of the table below.

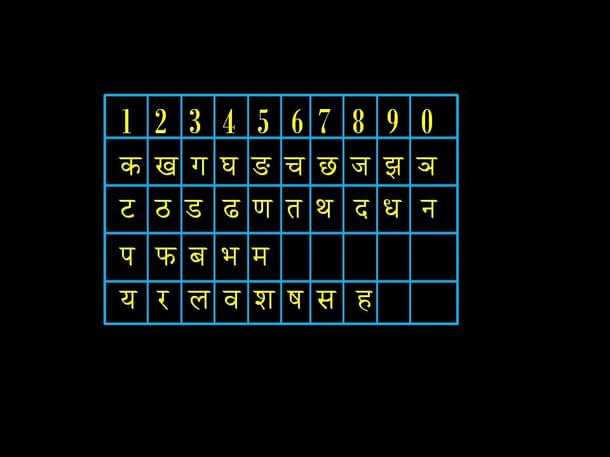
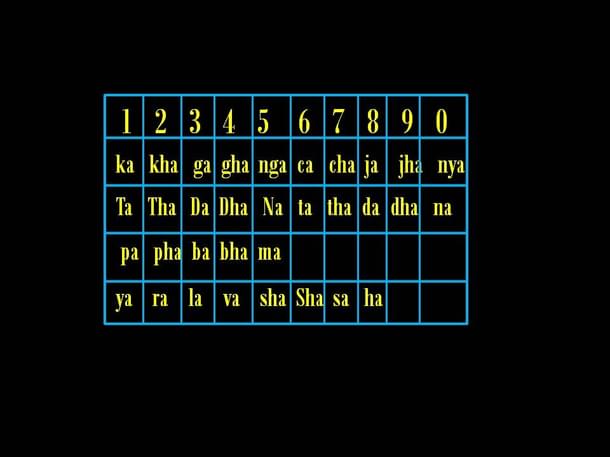
The name ka-ta-pa-ya-aadi क–ट–प–य–आदि comes from the beginning (aadi) letters in each row. Any number can then be represented by any one of two three or four letters.

For example, 1729 can be written as ka-cha-kha-jha ( कछखझ ) or pa-sa-ra-dha ( पसरध). Any vowel may be combined with each consonant, so pu-si-raa-dhu is the same as pa-sa-ra-dha.

This leads to interesting possibilities, where even meaningful word- sentences and puns can be formed based on names of numbers.

The Katapayadi system is popularly in use in notation of raga names in Carnatic music, in Venkatamakhi’s mela-karta naming system of the ragas, where the first two letters of the raga’s name represent the number of the raga.

For example, Maayamaalvagowla is the fifteenth raga because Maa is 5, ya is 1, so Maaya is 51 (LSD to MSD, here). Dhenuka is the ninth (09th) raga written as Dhe(9)-nu(0). Chaarukesi is the twenty-sixth raga - chaa (6) ru (2).