The Basics Of A Quantum Computer, Explained

In May 1981, physicist and Nobel laureate Richard Feynman gave a talk at a conference titled “Simulating physics with computers”, where he proposed the idea of using quantum computers to simulate quantum systems that are too hard to simulate using classical computers.

Feynman said “classical systems, in general, cannot simulate quantum systems efficiently” and offered the motivation to create a completely different computing paradigm, thus launching quantum computing as a field of study.

The ‘Inefficiency’ Of Classical Computers

Feynman may have had mostly quantum simulations in mind, but at present “quantum information science” includes sensing, cryptography, simulation, networking and computing.

Quantum computers are built with quantum bits or “qubits”, as they are popularly called, as opposed to the classical bits of present-day computers, which either take the value 0 or 1.

A qubit is any two-level system that can be physically implemented by various methods, like the Josephson junction, polarisation encoding, quantum dots, nuclear magnetic resonance, and electronic spin.

An example of a two-level system is an electron. It has a spin-up state and a spin-down state. The terms |1⟩ and |0⟩ (read as ket 1 and ket 0) are used to denote the electron in spin-up state and spin-down state respectively.

In quantum mechanics, these quantum states can be superimposed to form a new valid quantum state. We can write the new state as α|0⟩ + β|1⟩, where α and β are two complex numbers that are needed to specify the state of the system completely for a single qubit.

If we have N qubits, we need 2 raised to the Nth power complex numbers to completely specify the state of the system.

As an example, a 300-qubit system will need 2 raised to the 300th power complex numbers, which is greater than the number of atoms in the visible universe, proving Feynman’s point correct that classical systems, in general, cannot efficiently simulate quantum systems using classical computers.

Quantum Complexity, Quantum Algorithms And Speedups

The question now is, how many times is a quantum computer faster than a classical computer? Is it a million times faster or a billion times faster?

The answer is not so straightforward and lies in the complexity of a problem. Complexity theory looks at how difficult it is to solve a problem as the problem gets larger.

For example, the multiplication of two N by N matrices requires an operation that grows in complexity like N cubed with the size of the matrix.

Quantum computers are promised as a magic pill that will solve all our computing problems instantly, but that is not the case. The speedup depends on the type of problem we are trying to solve. The problems that are efficiently solvable by a quantum computer are categorised as BQP (bounded-error quantum polynomial time) complexity class.

Thus, for some computational tasks — for example, factorising a big number into its prime factors — quantum physics appears to provide an exponential benefit, but for certain other tasks — such as satisfiability or other ‘NP complete’ problems — the quantum benefits appear to be inherently more restricted, giving perhaps at most a polynomial speedup or sometimes even the benefits are still unknown.

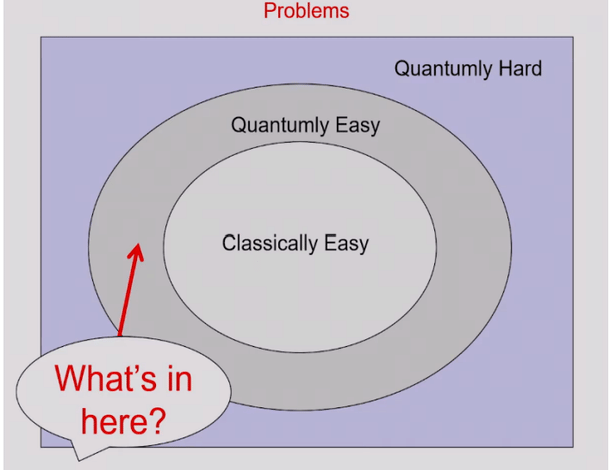
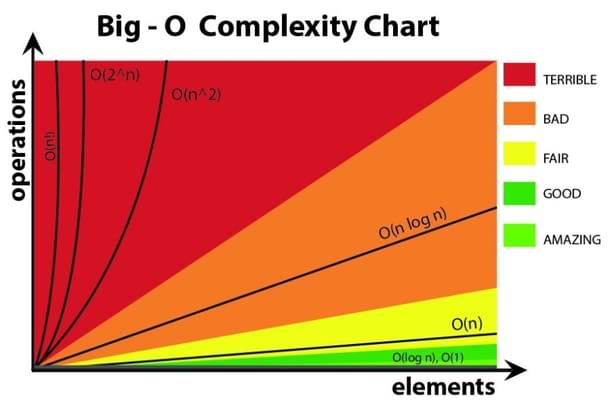
The point of quantum computers is to achieve better scaling of operations. For example, by taking a problem where the best-known classical algorithm has an exponential scaling (2 raised to the Nth power, 10 raised to the Nth power, etc) of operations with N and solving it using a quantum algorithm, for which the number of operations grow like N squared or N cubed or of similar complexity with N, thereby achieving huge speedups.

For example, physicist Peter Shor in 1994 proposed an algorithm for factorisation that provided exponential speedups over classical algorithms. Shor’s discovery of the prime factorisation algorithm had implications for cryptanalysis and caused rapid growth in the study of quantum computing. Today, several quantum algorithms have been developed in various areas, like quantum chemistry and quantum machine learning.

Measurement, Wave Function Collapse, And Multi-Qubit States

As described earlier, a qubit is a two-level system. It can be in state |0⟩, |1⟩ or a superposition of these states |ψ⟩ = α|0⟩ + β|1⟩, where |ψ⟩ is called the wave function.

Every quantum state is represented by a wave function. Here, α and β are probability amplitudes of the wave function, meaning if we measure the qubit, the probability that the outcome will be state |0⟩ is ||α|| squared and the probability that the outcome will be state |1⟩ is ||β|| squared.

It is important to note that the qubit is not secretly in state |0⟩ or |1⟩. Rather, it is in a superposition of both these states and, on measurement, the qubit collapses to either |0⟩ or |1⟩ state.

As the particle will be in the state |0⟩ or state |1⟩ after measurement, the probabilities associated with them will also add up to 1, that is ||α|| squared + ||β|| squared = 1.

Subsequently, if measurements are made on the same qubit, its state remains the same. For example, if we measure the state of a qubit and it turns out to be |1⟩, then if we measure the same qubit multiple times, we will always get the same state. This is called the collapse of the superposition, because the superposition state |ψ⟩ = α|0⟩ + β|1⟩ collapses to either |0⟩ or |1⟩.

Now, let us take a two-qubit system. If we consider two electrons in two hydrogen atoms, each electron can be in the ground state or excited state, making it a two-level system. If 0 represents the ground state and 1 represents the excited state, classically these two electrons together can be in four states: 00, 01, 10, 11. These represent 2 bits of classical information. In quantum mechanics, these two electrons will be in superposition of states denoted by |Ψ⟩ = α|00⟩ + β|01⟩ + γ|10⟩ + δ|11⟩.

A 2-bit classical register will only be able to store one of the four values, whereas in a quantum register, it is possible to store all the possible values simultaneously spanned by the qubits.

Quantum Entanglement And Spooky Action At A Distance

Quantum complexity is the reason why we think quantum computers will be faster than conventional computers. However, that also introduces the need for quantum error correction, which will be touched upon later.

These two central ideas rest on the concept of quantum entanglement. An important feature that distinguishes classical bits from qubits is that two or more qubits can be quantum-mechanically entangled. Those qubits which are part of an entanglement correlate with each other to form a closed system.

A 2-qubit system can have several entangled states, for example 1/√2(|01⟩ + |10⟩) is an equal probability entangled state. It means that there are equal probabilities (1/√2) squared = 1/2 of measuring either product state |01⟩ or |10⟩. These entangled states cannot be expressed in terms of |0⟩ or |1⟩, making them inseparable.

Here, inseparable doesn’t mean separating the qubits physically; qubits even physically separated can still be entangled.

Now, imagine we have two entangled qubits that are separated. One is given to Alice and the other to Bob. If Alice makes a measurement and obtains state |0⟩, then Bob’s measurement will be opposite to that of Alice, that is, state |1⟩, because in the entangled state 1/√2(|01⟩ + |10⟩), if Alice measures |0⟩, then Bob must measure |1⟩, as |01⟩ is the only state where Alice’s qubit is |0⟩ and Bob’s qubit is |1⟩.

Whatever Alice measures, Bob will measure the opposite with a perfect correlation, however far apart they are present.

Albert Einstein called entanglement “spooky action at a distance” due to its strangeness and this lies at the heart of quantum computing.

It has been shown that the presence of multipartite entanglement, with a number of parties that increases unboundedly with input size is necessary if the quantum algorithm is to offer an exponential speedup over classical computation.

This was the first of two parts on quantum computing. The next part will cover quantum communications, cryptography, government initiatives, and why quantum computers are hard to build.

This article has been published as part of Swasti 22, the Swarajya Science and Technology Initiative 2022. We are inviting submissions towards the initiative.

Also read:

National Science Day: The Raman Effect And One Of Its Key Applications, Explained