Magazine
The Extraordinary Schools Of Mathematics In India
Rajeev Srinivasan
Oct 01, 2018, 03:38 PM | Updated 03:38 PM IST
Save & read from anywhere!
Bookmark stories for easy access on any device or the Swarajya app.


From anecdotal evidence, one could make a case that Indians have a certain 'mathematical gene'. This concerns things as trivial as our ability to do simple arithmetic in our heads (although this skill may be atrophying with the ubiquity of smartphone calculators) which so impresses check-out clerks in America when we can tell them they have made a mistake in toting up our bill. It also concerns things as sublime as the extraordinary equations of Srinivasa Ramanujan: there is no other word to describe them sometimes other than as 'beautiful'. Staggering, too, maybe. How on earth did he know this? His answer, of course, was that it was intuition, based on his connection to his ishta-devata, the Goddess Namagiri.
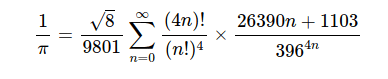
But there is some evidence that we do have a mathematical bent. And this has resulted in some remarkable results in several related areas: formal languages and astronomy as well as pure mathematics. This may also be an example of the gap between invention and innovation: the application of a brilliant new idea in these technical fields may take a long time, until the environment is ready for it.
There is the case of that magnificent results attributed to Madhava of Sangamagrama, some time in the 1300s CE. Take also the circumstances surrounding the establishment of his Academy, which is now called the Kerala School of Mathematics and Astronomy, although that was certainly not what it was referred to as in its prime: it was, in all probability, a Vedic pathasala.
The great centers of teaching and learning were all in the north of India. Kerala is not known as a hotbed of mathematical scholarship. So how come this school was established there, and had a series of major mathematicians and astronomers in roughly the 1300 to 1500 CE timeframe? The answer lies in two things: the sacking of Nalanda in 1182 CE by Bakhtiar Khilji, and the establishment of the Vijayanagar Empire.
The great universities, such as Nalanda, Takshasila and Vikramasila, all ceased to be around this time. Scholars fled; there was continuous warfare in north India for the next few centuries, and there was no opportunity for scholarship to thrive. But Vijayanagar protected southern India; and thus the flowering of the Kerala School. It is notable that after Vijayanagar fell at the Battle of Talikota in 1565, the Kerala School too declined; the coup de grace, it appears, was delivered by later invasions by Hyder Ali and Tipu, which put paid to the kingdoms that had funded and supported the scholars.
That history apart, the fact is that a largely unsung group of mathematicians such as Madhava, Parameswara and Nilakantha Somayaji, who wrote in Sanskrit and in Malayalam, arrived at the first known results about infinite series for various irrational numbers, most notably the trigonometric functions that now go by the names sin, cos, tan, arcsin, arctan etc., as well as for pi. Here is an (unauthenticated) portrait of Madhava of Sangamagrama (which is now Irinjalakuda, close to the great historic port of Muziris), as well as some of their results. These simple and intuitively appealing series are obviously converging, and can be used to calculate accurately to arbitrary numbers of decimal places.
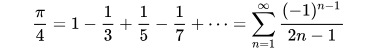
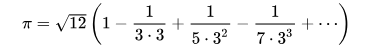

There are a few points to note: one is that Madhava, Parameswara and Nilakantha clearly understood irrational numbers, the notion of infinite series, and most significantly, the notion of computation-friendly series that converge more or less rapidly. It is quite possible that it was only in India, where the notions of infinity, irrationality, etc. would not have raised eyebrows (as compared to medieval Europe where the authorities would have stepped in to nip such heresies in the bud) that such ideas could rake root.
There is also the very idea of epistemology, that is, the creation of knowledge. There were two interesting aspects facets of this in India. One is that knowledge was created on a dry, theoretical basis, but for practical applications. The second is that the knowledge that was so created was considered Commons, freely available to society at large, instead of being held as revenue-generating Intellectual Property (as is common in the patent regime today that views IPR as a private good guaranteed to be inviolable by the State, at least for a time).
I have been reading some work by that intriguing public intellectual, Nassim Nicholas Taleb, where he argues that the Greeks were driven by theory, while the Romans were driven by practice. I am not so sure of that distinction, but it is clear that Hindu mathematicians and astronomers were driven by practical considerations: the right times for planting, harvesting etc., or the building of ritual falcon-shaped fire altars based on precise astronomical measurements (see the work of the scholar Subhash Kak on the astronomical code of the Rg Veda).
Quite interestingly, the infinite series were themselves put to great use, although not in ways imagined by Madhava et al. To put it simply, their work enabled both the Industrial Revolution and the spate of European colonialism: two events of staggering importance. Unfortunately, but not surprisingly, the traditional narrative does not give credit to the Kerala School for its ground-breaking results. The series discovered by them still go by the names 'Taylor' and 'McLauren' series, although those gentlemen merely re-discovered the series, and by the normal rules of primogeniture, the series should be called 'Madhava-Taylor' etc. A vestige of European derision for Hindu civilization, this should be remedied at least in Indian textbooks, and a concerted effort made to correct it.
The story of the Kerala School's manuscripts is yet another example that suggests that globalization is not so new a concept as one might think. In this context, let me make a digression: there is the unproven conjecture by S Kalyanaraman of the Sarasvati Research Center in Chennai about the ancient Tin Route, that preceded the famous Silk Route by a couple of thousand years.
As per his hypothesis, there was an enormous supply cum demand chain that went from Haifa in Israel to Hanoi in Vietnam: tin was mined in the Malay peninsula, processed locally, transported via the Indian Ocean to ports like Lothal in the Sarasvati region, to create high-quality bronze artifacts, jewelry (including high-reflectance metal mirrors) and images, which were then sold across much of West Asia as early as 3000 BCE. This could explain India's prosperity by 0 CE, the start of the Common Era. In comparison, the Silk Route was no earlier than 1000 BCE.
Besides, it suggests that continent-spanning supply chains and expert sea-borne trade are not 20th century CE inventions. India clearly was a naval power that long ago, including both river-borne trade and ocean-going vessels that could navigate the high seas.
Incredibly, that navigation of the high seas, out of sight of the land, was something that European sailors could not do until about 1700 CE, and that was one of the innovations that the infinite series discovery led to. With Madhava's series, it is possible to create tables of trigonometric functions, and indeed such tables, I was astonished to learn from a US Navy submarine lieutenant, are standard issue even today on their boats. Why? These are disaster-recovery backups to the Global Positioning Satellites (GPS) should they ever fail. With the tables, and accurate clocks and sextants, it is possible to precisely locate the ship on the surface of the earth, in latitude and longitude.
That innovation, therefore, perversely resulted in the ability of Europeans to send their warships to India and other nations and to colonize them. Add to this their other innovation -- the ability to make lots of guns, as a result of the Industrial Revolution -- and the rest is history. Hitherto minor European nations (such as Britain, France, the Netherlands, Portugal and Spain) were able to, in a short few years, to establish lucrative empires where they drained off the wealth of the subject populations.
The Industrial Revolution, too, in an indirect way, could be said the result of Madhava's infinite series. There is considerable circumstantial evidence -- this is the result of research by C K Raju and George Joseph (though unfortunately the collaboration ended badly, with the former accusing the latter of plagiarism) that suggests that the Kerala School's manuscripts were taken to the Vatican by Jesuits who had arrived in Kerala to study the local calendar.
At that time, as now, the Hindu calendars were precise and correct (thanks to a tradition of astronomy and no dogma about the Earth being the center of the Universe), whereas the Julian calendar then in use in the West was hopelessly messed up: it was clearly inadequate to correctly predict even the seasons. The Jesuits studies the Hindu calendars and other mathematical work, and it is virtually certain that these formed the basis of the revamped Gregorian calendar (let us note that they had to add an entire month to correct the accumulated errors of the Julian calendar!).
As part of this, conjectured Professors Raju and Joseph, the Madhava manuscripts were also taken to the Vatican, from where their knowledge spread all over Europe. The infinite series are the basis of the Differential Calculus, which is the firm basis on which the Industrial Revolution, and indeed much of engineering and a good bit of science stand to this day.
It is said the Isaac Newton and Gottfried Liebniz invented the calculus independently and simultaneously. Well, a good explanation for that might well be that they both had read the Kerala manuscripts at the Vatican library and got inspired therefrom, and added the last bit that the Kerala School had missed. They clearly stood on the shoulders of giants, and credit should be given where it is due. Thus the Kerala School's invention (or discovery) led to the innovations of the Industrial Revolution, that gave Europeans their competitive advantage over the last two or three centuries.
There is yet another connection worth noting: how the conquest of Bengal most probably created the venture capital (i.e. risk capital) that encouraged the Industrial Revolution. It is surely an arresting coincidence. In the 17th century, the four greatest centers of industry in the world were four river deltas: the Kaveri delta in Tamil Nadu, the Brahmaputra delta in Bengal, the Pearl River and Yangtze River deltas in China. Together, they probably accounted for some 60% of world GDP.
It was precisely those two delta that the British targeted as their first bases. In 1757, there was the Battle of Plassey, which gave them control over Bengal. The Industrial Revolution started just a few years later, according to William Digby: the flying shuttle, 1760; spinning jenny, 1764; the power-loom, 1765; the steam engine, 1768. Coincidence? Perhaps. But the analogy with the astonishing innovations of Silicon Valley and the venture capital community there is interesting.
Of course, it would be ridiculous to assert that all this happened entirely because of the Kerala School of Mathematics. However, it is equally foolish to not acknowledge that their work gave a boost to the Europeans.
What is really saddening, however, is that there is almost no mention of this extraordinary school of mathematics in any textbook in India. If we do not respect some of the greatest mathematical geniuses of medieval times, can we realistically expect others to do so?
Rajeev Srinivasan focuses on strategy and innovation, which he worked on at Bell Labs and in Silicon Valley. He has taught innovation at several IIMs. An IIT Madras and Stanford Business School grad, he has also been a conservative columnist for twenty years.




