News Brief
Fibonacci Sequence: The Connection To Vedas, Role Of Sanskrit, And A Look Into What Drove Science In Ancient India
Yaajnaseni
Nov 27, 2019, 10:20 AM | Updated 10:19 AM IST
Save & read from anywhere!
Bookmark stories for easy access on any device or the Swarajya app.
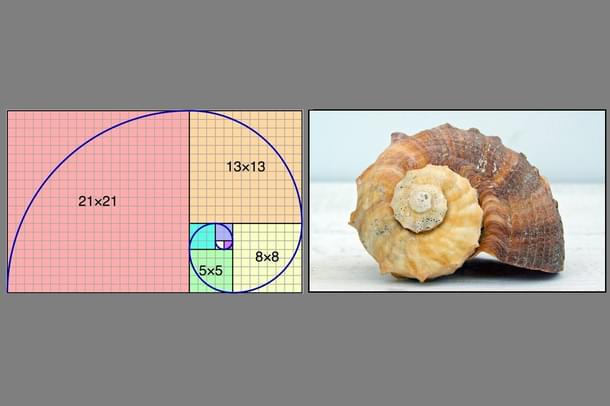
The 23rd of November is celebrated as ‘Fibonacci day’ because when the date is written in the mm/dd format (11/23), the digits in the date form a Fibonacci sequence: 1,1,2,3.
The Fibonacci sequence - a sequence of numbers with an inherent pattern - appears surprisingly often in nature. Their appearance is so fascinating that an entire journal is dedicated to the Fibonacci numbers, in the Fibonacci Quarterly.
The name ‘Fibonacci’ is due to a 13th-century Italian mathematician Leonardo of Pisa, who later came to be known as Fibonacci. However, what we Indians popularly call ‘Fibonacci numbers’ find their earliest mention in the 2nd century BCE work of Acharya Pingala.
Fibonacci is also credited with introducing Indian numerals in the West, and in his historic work, Liber Abaci, he expresses his attraction to learning the Modus Indorum - the method of the Indians.
What Are Fibonacci Numbers?
In the Fibonacci sequence, each number is the sum of the previous two, starting from 0 and 1. Therefore, the sequence looks like this:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on.
The ratio of consecutive Fibonacci numbers approaches the ‘golden ratio’ or phi = 1.618. (In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities; that is, (a+b)/a = a/b; if a is larger than b).
The Fibonacci sequence is manifested in the pattern of branching in trees, in the arrangement of leaves on a stem, in the fruit sprouts of a pineapple, etc.
An Indian Institute of Science paper investigated the pattern on the conch shells and found that it satisfied the Fibonacci patterns. The shape of galaxies, along with the arrangement of piano keys also follows the Fibonacci pattern.
Fibonacci And The Sanskrit Connect
Before we discuss the work of Rishi Pingala, it is crucial that we devote some time to understanding the role played by the Sanskrit language in making scientific work in ancient India possible.
The readers will soon discover the connection with the Fibonacci.
Sanskrit is the language of not only several great works of literature like Mahabharata but also of mathematics, medicine, sexual and mental well-being, astronomy, philosophy, and so on because it is the most suitable language to transmit knowledge.
An article on Guruprasad’s Portal beautifully brings out these aspects of the Sanskrit language.
The article argues that the rules of the language were designed in such a fashion that poetry became an efficient medium of conveying scientific principles. Remember that the Vedic civilisation was dependent more on experiential learning and oral transmission, therefore an efficient language was key.
This was best summarised by Jagadguru Shankaracharya Swami Bharatikrishna Tirtha (the Shankaracharya of Govardhana matha in Puri, Odisha, from 1925 to 1960):
“In order to help the pupil to memorise the material studied and assimilated, they made it a general rule of practice to write even the most technical and abstruse textbooks in Sutra or in verse [format] (which is so much easier -- even for the children -- to memorize).”
When we look at the knowledge that has survived through centuries, including the subject we are currently discussing - Fibonacci - we must remember that the resilience of the ancient language is to be credited for the same.
One example of Sanskrit poetry that shows how the language went beyond aesthetics of the words is Magha’s Shishupala Vadha. The seventh-century poet’s work is taken as one of the Maha-Kavyas in the Sanskrit language.
In the third stanza, Magha uses only 4 consonants. In the 66th, he uses just two and in the 114th stanza, Magha uses just one consonant!
दाददो दुद्ददुद्दादी दाददो दूददीददोः ।
दुद्दादं दददे दुद्दे दादाददददोऽददः ॥
Using just one consonant, Magha conveys the following to the reader:
“Sri Krishna, the giver boons, the destroyer of the evil, the purifier, the one whose arms destroy the wicked who cause suffering to others, shot his powerful arrow at the enemy.”
Magha also creates the most exquisite palindromes.
In the 44th stanza, each line has a palindrome. The 88th stanza is a palindrome as a whole - syllable-for-syllable:
तं श्रिया घनयानस्तरुचा सारतया तया ।
यातया तरसा चारुस्तनयानघया श्रितं ॥
The 34th stanza is the 33rd stanza written backward, conveying a totally different meaning.
The 27th stanza, which Martin Gardner called the “the most complex and exquisite type of palindrome ever invented” in his book Mathematical Circus, reveals the same sequence of syllables when read forwards, backwards, down, or up:
सकारनानारकास-
कायसाददसायका ।
रसाहवा वाहसार-
नादवाददवादना ॥
sa kā ra nā nā ra kā sa
kā ya sā da da sā ya kā
ra sā ha vā vā ha sā ra
nā da vā da da vā da nā
And the lines reversed :
nā da vā da da vā da nā
ra sā ha vā vā ha sā ra
kā ya sā da da sā ya kā
sa kā ra nā nā ra kā sa
This stanza is called ‘Sarvatobhadra’, that is ‘perfect in all directions’.
The syllables of the 29th stanza form the shape of a “drum”.
सा सेना गमनारम्भे
रसेनासीदनारता ।
तारनादजनामत्त
धीरनागमनामया ॥
Here’s how it works: read the first line sequentially; then starting from the left-most syllable on the first line, follow the shape of a U/V to move to the subsequent lines; you will find that you are reading the same syllables as that of the first line!
sā se nā ga ma nā ra mbhe
ra se nā sī da nā ra tā
tā ra nā da ja nā ma tta
dhī ra nā ga ma nā ma yā
Also, an inverted drum is visible between the first and the last rows. This has the same syllables as the last line. In addition, three drums can be seen in the top two lines (inverted-upright-inverted) - with same syllables as the second row. The bottom two rows also have three drums (upright-inverted-upright) - these make for the third line.
Therefore, no matter on what syllable one puts her finger on, it is part of a drum structure, along with a row.
Similarly, there are stanzas that can be arranged into the fascinating shapes of a sword, zigzag, etc.
The 120th stanza ends with a wheel design with spokes. It is called chakrabandha, wherein the syllables can be arranged in the form of a wheel with six spokes.
Undoubtedly, some mathematical planning would have been required before writing out these verses. One is inevitably reminded of the graphs in mathematics classes while looking at these.
Another fascinating work is Daivagya Surya Pandita's Rama Krishna Viloma Kavyam which when read from the first letter to the last gives the story of Sri Rama and when read in reverse, of Sri Krishna.
There are several other examples of the creative usage of Sanskrit language that mixes devotional literature with mathematical principles.
Pierre-Sylvain Filliozat calls such compositions in the verse form, “the unexpected processes for the exposition of technical matter that have been the rule in all the vast Sanskrit mathematical literature.”
Filliozat, in his work, elaborates on the “techniques of oral transmission of the text of the Vedas, and the earliest exposition of geometry in the context of Vedic rites of building brick altars, the numeration system, the arithmetical and geometrical concept of square.”
Sanskrit Prosody Or Chandas
Chandas is the study of Sanskrit verses and their rhythmic structure, called poetic metres. Chandas was used to maintain the purity of the text (and integrity of the principle mentioned via the text).
The earliest known treaty of the Chandas Shastra is written by Acharya Pingala. The 10th-century mathematician Halayudha wrote a commentary on the Chandas Shāstra and expanded it.
Chandas Shāstra presents the first known work of a binary numeral system. Instead of 0 or 1, Acharya Pingala calls it Laghu (light) and Guru (heavy) syllables.
The Guruprasad Portal article uses the example of music. Laghu syllables are those that need one beat and Guru syllables are those that require two beats. Tabla players use the same concept, where they call short syllable as “Dhin” and long syllable as “Dha”.
The article states that a poet can create an exquisite work of poetry if he plans in advance how to arrange the Laghu and Guru syllables in each shloka, and how many such combinations are possible for each shloka.
Let’s use 0 and 1 for Laghu and Guru respectively, where 1 as Guru requires two beats.
For a shloka with just one beat, the number of combinations of Laghu and Guru possible is one (0 only). For a shloka with two beats, the possible combinations are two (00, 1). And for a shloka with three beats, the number of combinations possible are three (000, 01, 10).
For a shloka with four beats, the number of combinations is five (0000, 001, 100, 010, 11). For a shloka with five beats, the possibilities are eight (00000, 1000, 110, 0001, 011, 0010, 0100, 101).
Do you see the Fibonacci sequence in the underlined numbers above? Fascinating, isn’t it?
Pingala also conceptualised a pyramid of stacked numbers that he claimed converges to the golden mean, calling them Maatra Meru, Sumeru.
Like Pascal’s triangle (written hundreds of years after Pingala), the Maatra-meru of Pingala consists of a pyramid in which adjacent proportions converge towards the golden ratio.
Several later scholars built up upon Pingala’s Chhanda Shastra. Carnatic music has also imbibed the principle of the Fibonacci series.
The fifth-century scholar Varahamihira uses Pingala’s work in his theory of binomial coefficients. Halayudha's commentary (tenth century) includes a presentation of Meruprastāra. Pascal’s triangle, therefore, is also known as Halayudha triangle.
A clear exposition of the Fibonacci series is provided by Virahanka (700 CE). Unfortunately, his original work is lost and is now known through a quotation in the work of the 12th-century mathematician, Gopala. 11th-century Ratnakarashanti's Chandoratnakara is another example.
The works of Pingala and Varahmihira were related to their own fields, but the 12th-century scholar, Acharya Hemchandra, a Jain scholar in the court of the Chalukyan king Kumarapala, wrote a comprehensive commentary on the Fibonacci numbers. This was around 50 years before Fibonacci.
Sanatana Epistemology
With the above discussion, one needs to see the principle of ‘unity in diversity’ visible in the Sanatana epistemology, where Jnana (knowledge) is not just food for the mind, but also for the soul.
Unfortunately, our modern education has conditioned us to label our traditional expressions of knowledge as ‘superstitious’.
We must certainly be cautious against pseudo-science but we must also be open-minded enough to accept that the knowledge about human existence can be in various forms and expressions, at least with reference to the saint-scholars mentioned above.
The ace mathematician Srinivasa Ramanujan, a deeply religious Hindu, credited his acumen to his Goddess Mahalakshmi of Namakkal and said that by her grace he could see complex mathematical content unfolding before his eyes.
Those of us who are not well-versed with the Sanatana way, would mistakenly picture the above, thanks to Bollywood perhaps, as a dramatic scene filled with “magic” that replaces the hard mental work required to work out those equations.
(Spiritual path is certainly deeply personal, mystical and full of inexplicably blissful and profound experiences. However, here the term “magic” is used to refer to the fetishisation and misrepresentation of the former as an overly dramatic short-cut to attaining money, fame, power or revenge.)
This couldn’t be farther from the truth. When Ramanujan mentions the visions of complex mathematical content, it doesn’t refer to something “magical” that bypasses the intellect and mind of Ramanujan.
It simply reflects the Sanatana way of learning -- moving from the ‘part’ towards the ‘whole’ -- with sometimes the bigger picture offering a clue as to what’s the next step, and the next step taking us towards the bigger picture.
Here the bigger picture is the Ultimate Truth; for Ramanujan, it manifests as the loving mother Mahalakshmi, and each mathematical equation as a step towards it, as it unravels the truth of our existence more and more.
Each mathematical equation shows that the laws of existence are beyond and above the narrow identities and afflictions that one mistakenly attaches oneself to, and drives Ramanujan to shed the ego, the aham associated with his samsaric existence. It liberates Ramanujan to understand things beyond physicality.
This is why Ramanujan said, “An equation for me has no meaning, unless it expresses a thought of God.”
The principle that several jnanis of the Sanatana tradition have propounded -- that by performing mere external rituals and dressing up as a Sadhu one cannot attain Sadgati, -- is clearly affirmed here.
A person who simply claims to be a man of religion has no monopoly over spiritual well-being and progress. A biologist, mathematician, physicist, medical researcher are much ahead so long as they remain committed to finding the truth, and resist ahamkaar (ego, self-indulgence, narrow-mindedness).
True, a scientist limits his domain to begin his research while the Ultimate Truth is limitless. One such limitation is, for example, logic. The men of science refuse to follow illogical or irrational leads. But as one progresses, they come to realise how such limitations themselves dissolve, merge and evolve.
The illogical becomes logical and vice versa, and so do their understanding of the limitations of right and wrong, correct and incorrect. Such is the path of the truth, it liberates one from assumptions and the stereotypes (Punya-Apunya vivarjit panthah).
The key is to remain open-minded and committed to the truth -- and not be diverted by, say, ideology, identity, “magic” or worldly limitations.
We find several works, say Vatsayayana’s Kama Sutra or Charaka’s treatises on medicine that mention things and actions that the scriptures on social conduct prohibited.
For example, Kama Sutra elaborately mentions love-play in a river, whereas the same is prohibited (under a broad category of prohibition of polluting the river with bodily excretions).
Similarly, Charaka mentions the physiological effects of consuming cow’s meat, which contemporary texts prohibit.
This is because both Vatsyayana and Charaka were committed to finding the truth in their own domains. They were not writing a book on social or moral conduct, but on their own subject-matter.
It was the job of an administrator to bring out the rules of conduct and decide the rules of conduct based on various considerations, balancing different interests (including their own, perhaps).
An example would be Manusmriti, which was written by a king and not a Brahmana scholar.
Both Vatsyayana and Charaka strove to describe things as they are. Vatsyayana’s goal is to provide a treatise for sexual well-being while Charaka’s is to provide one for physical well-being.
The insights from such works were incorporated into customs and traditions, through a downward filtration process, albeit, tweaked, amended and presented as per the politico-social conditions by those in power.
As expected, this relationship, between those who discovered and those who implemented was not without its tensions. Perhaps, the vast diversity among both the groups provided for mitigation of crises quickly and at a suitable level.
Another factor could be the heavy exchange of knowledge between the two groups. For example, texts mention several scholar Rishis, from their Ashramas in remote areas, visiting kingdoms and having discussions with the kings.
On the other hand, kings as well as all grihasthas took Sanyasa and visited such Ashramas in their old-age.
It is also important to note that the former category of works - written by intellectuals and not administrators (or for administrative purposes) - encouraged experimentation, debate, and dissent.
On the other hand, the administrative works, by design, carried authority and often proposed divine consequences for bad actions, to ensure compliance.
Today, many of the insights of out scholar Rishis are only available through administrative works and folk practices, which means, we would have to sift through what has become irrelevant with the change of times to reach the kernel of truth and decide our Dharma - the correct course of action suitable for our present times.
Conclusion
A great lesson we can take from our Rishis is to separate the domain of knowledge from the domain of politics.
The ideologically-biased knowledge-ecosystem in post-independence India has resulted in polarisation, bitterness, identity politics and triumph of power-politics over the truth, as people have lost the trust in the intellectual-class.
The latter are increasingly seen as ideologues and hypocrites who criticise their own nation and lack nationalism but wag their tails to get the citizenship from the international-elite class of opinion makers.
Pingala uses the language of Sanskrit, Hemchandra and Ramanujan, the language of numbers, and bhakti-sants, the language of surrender and love. They are separated by centuries yet they unite us as the fresh leaves of the same grand tree with several branches, and roots going back several millennia.
I will end this piece with an example from the life of Acharya Hemchandra, a Jain scholar in the court of a Shaiva king, Kumarapala.
When visiting a temple with the king for an inauguration, Hemachandra bowed before the Shiva Lingam in reverence and said:
“I bow down to him who has destroyed the passions like attachment and malice which are the cause of the cycle of birth and death; whether he is Brahma, Vishnu, Shiva or Jina.”
A 25-year-old IIT alumna with deep interest in society, culture and politics, she describes herself as a humble seeker of Sanatana wisdom that has graced Bharatvarsha in different ways, forms and languages. Follow her @yaajnaseni





