Culture
Indian Astronomy And Mathematics: When Kerala Became The Locus Of Genius
R Gopu
Feb 19, 2020, 09:51 AM | Updated 09:51 AM IST
Save & read from anywhere!
Bookmark stories for easy access on any device or the Swarajya app.


This piece is the last in a series of essays on Indian astronomy and mathematics. Read the previous piece by the author here.
The Classical Era Continues
For centuries after Bhaskara, the classical era continued. The Ganita Kaumudi of Narayana Pandita is a fascinating book, with an interesting structure and several novelties. Like Mahavira, he gave both rules and a series of examples. He expanded Aryabhata’s formula for sum of series of numbers, their squares, and cubes, to any arbitrary power.
Effectively, he provided the formula
(Sn)r = [n(n+1)(n+2)…(n+r)] / [1.2….(r+1)]
Narayana also expanded on the meru prastaras (Pascal’s triangles) of Pingala and Hemachandra into more elaborate versions. Permutations, combinations, areas and volumes of more complex geometric shapes were other areas of exploration and explanation.
His famous novelty was magic squares, squares filled with numbers so that each row and column add up to the same number. He explained procedures to create magic squares of desired sizes, how to fill them up for a given total, and certain fascinating variations, including use of negative numbers.
He extended this to magic rectangles, and other figures, like squares within squares, triangles within triangles etc. He also devised many more such shapes like vajra (diamond), padma (lotus), padmavrtta (lotus circle), mandapam (canopy), sadashra (hexagon), dvaadashaashra (dodacehedron) etc filled with such numbers.
These are explorations with perhaps no practical applications, especially in astronomy.
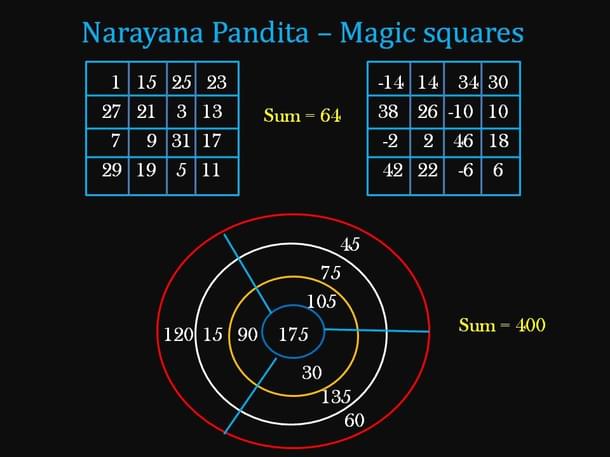
Later Jaina mathematicians, Dharamanandana and Sundarasuri, continued explorations on magic squares and similar arrangements.
But from the fourteenth century, Kerala became the locus of several new siddhaantas, bhaashyas, karanas etc., that it is now called the Kerala school of mathematics.
The Kerala school
Shortly after Aryabhata, a mathematician called Haridatta had composed a work title Parahita Ganita based on Aryabhatiyam. After that we seem to have a vacuum in Kerala until Madhava (c 1340 AD) of Sangamagrama (Kudalur in Malayalam). What followed is an astonishing continuity of the guru-shishya parampara from Govinda Bhattatiri to Rajaraja Varma.

Madhava was famous as a skilled instrument maker. Indian historians of mathematics consider him the pitamaha of the Kerala school. Perhaps, his most famous contribution is sums of infinite series.
To calculate the circumference (paridhi) of a circle, said Madhava, we must multiply the diameter (vyaasa) by four times one minus tri-sharaa-aadi-vishama-samkhyaa-bhaktam-rNam. A phrase of compactness, which Aryabhata would have enjoyed. In other words, a sequence of odd (vishama samkhyaa) denominators (bhaktam) starting (aadi) with three (tri) and five (sharaa). The word sharaa here is a bhutasamkhya (see third essay) word for the five arrows of Manmatha, whose archery takes precedence over Rama and Arjuna and even Tripurantaka, in this case.
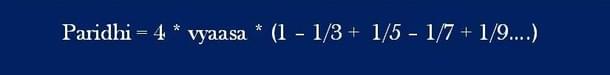
The sum of the series in the brackets adds up to π/4, and is famous as the Gregory Leibniz series.
Madhava’s series was quoted and a proof (upapatti) also given a century later by Jyeshtadeva.
Parameshvara – Like Brahmagupta providing a sphuTam to Paitamaha Siddhaanta, Parameshvara observed that over time, predictions of earlier astronomers did not agree with observed positions based on calculations. In such a situation, he observed, one must adjust one’s methods and calculations, because planets and stars will conform to them.
He titled his book Drg Ganitam. This title, which means Observed Calculations, is a popular phrase for jyotisham in south India, though the author himself has faded from public memory. His shishya NilakanTha referred to him as Paschimaam Bodhi, the western scholar.
Nilakantha Somayaaji – More unknown than even Brahmagupta, was a polymath like Varahamihira. He was a scholar of Shad darshana (the six philosophies of Hinduism, and also in vyaakarana, chandas, the Bhagavata and various such literature. He also studied Vedanga Jyotisha, Pancha Siddhaantika, Brhat Samhita etc.
This historical curiosity and scholarship may have shined in other scholars, too, but in Nilakantha, we have contemporary evidence. He was also a prolific composer, of several texts.
He was a friend a Sundararaja, a jyotisha of the neighboring Tamil Nadu, and took the effort to compile a written list of answers for questions posed by the former, compiled into a book called Sundararaja Prashnottara.
Aficionados of European science may be reminded of the extensive correspondence of Franklin, Newton, Darwin, Humboldt etc.
A ninth century mathematician called Virasena in his commentary Dhavala gave this equation, that the sum of all powers of 1/4 is 1/3. One sees the reflection of this in Madhava’s several infinite series. Nilakantha questioned this apparent absurdity. How does the sum of this infinite series increase to that finite value (1/3), and that it reaches finite value?
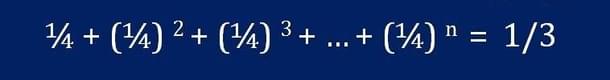
He reasoned and explained it by deriving the following sequence of results:
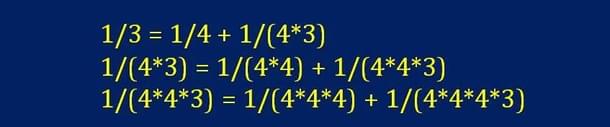
As we add more terms, argued Nilakantha, the difference between 1/3 and the powers of 1/4 become extremely small, but never zero, unless we add terms up to infinity. In the 20th century, Ramanujan revelled in such series.
Quasi Heliocentric theory NilakanTha’s questioning of an assumption of planets’ latitudes (vikshepa), and his subsequent discovery was truly astronomical (pardon the pun). From the siddhantas through Bhaskaracharya, all astronomers used a slightly different method to calculate the latitudes of Mercury (Budha) and Venus (Shukra), than they did for the other planets. This niggled most of them, as “inappropriate”, especially Bhaskara, who then consoled himself with Prthudaka Svami’s explanation.
But NilakanTha questioned this acceptance, and modified his computation, and effectively the orbital model for these planets. He came to the conclusion that these two planets revolve around the Sun (but in his model, the Sun still revolves around the Earth).
The geometrical argument is too complicated not only for this article, but even, perhaps, for those who are not astronomers, so I will only present a visual illustration of his model here.
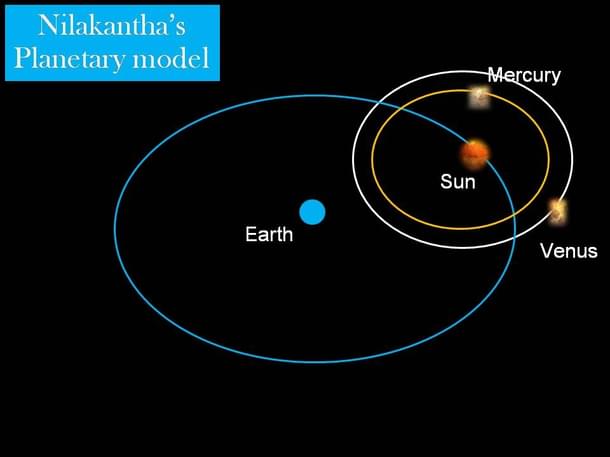
Effectively, NilakanTha formulated a quasi-heliocentric theory: sun centric for inner planets, and earth centric for everything else.
Jyeshta Deva, a junior of Nilakantha, wrote a work called Yuktibhaasha, in Malayalam, not Sanskrit. He extensively dealt with several proofs and also developed the theory of infinitesimals to greater refinement and sophistication.
Modern Era
The modern era was introduced gradually into India, with the advent of the East India company, and the influx of European scientific discoveries it brought along.
I’ll refrain from delving into the astronomical experiments the Europeans themselves conducted here, including the establishment of the Madras observatory, the Madras meridian, observations of Venus transit, the discovery of Helium etc.
Sawai Jaisingh’s Jantar Mantars are, perhaps, the most famous observatories in India, and really belong to the modern era. He was also instrumental in commissioning translations of Euclid and Ptolemy from Persian.
The most fascinating ganaka or siddhanta acharya of the modern era was Pathani Samanta Chandrasekhar, of Orissa. Utterly unaware of the European advances in astronomy including telescopes, electricity, gravity and optics, or even of the Madras observatory, and apparently not even aware of the Kerala school, he independently discovered the quasi helio-centric theory of NilakanTha Somayaji.
He also made several corrections and improvements to Bhaskara’s Siddhanta, using only the naked eye, besides developing his own new instruments. His book Siddhanta Darpana, with 2,500 slokas, was published by PC Ray.
He is the only jyotishaacharya of whom we have a genuine portrait picture. The Bhubaneswar observatory is named after him.

Sir William Jones, judge of the Supreme court of Bengal, founder of the Asiatic Society of Bengal, discoverer of the Indo-European family of languages, translator of Manu Smriti and Shakuntalam into Sanskrit, rediscoverer of Pataliputra, ad infinitum, also declared that India gave the world algebra.
Why we learn in school about FaHien and Hiuen Tsang, al Beruni and ibn Batuta, but nothing of this giant of Indian scholarship, I’ll never know.
Some of us Indians possess the same myopic prejudice against such European stalwarts as the haughty colonialists did of us lesser Indians. It may also be cognitive dissonance.
The Asiatic Society and such similar institutions like the Madras Literary Society produced extraordinary scholarship about several aspects of Indian history and culture, including astronomy and mathematics.
Henry Thomas Colebrooke, George Thibaut, John Playfair, Burnell, Burgess, and such other European scholars translated, analyzed and compiled the history of Indian sciences and exposed them to the world.
Charles Whish, and his collaborators John Warren and George Hyne played a significant role in bringing to light the Kerala school in the early nineteenth century. This was also the period when English effectively replaced Sanskrit as the primary language of science in India.
The spectacular advances brought about by the Industrial revolution, and subsequent scientific advances in Europe, and the corresponding rise of European intellectual and military supremacy, drowned out the accomplishments of Indians in the past (and other cultures as well).
The rest of the world is catching up in application of technology, but is stall far behind in the curiosity and spirit that drove discoveries and inventions. That is now changing.
European orientalists did not work in isolation. Indian pandits, like Sudhakara Dwivedi, Chidambaram Iyer, and numerous others helped translate Sanskrit texts into English, French and other languages.

In the twentieth century, scholars like Bibhutibhushan Dutta and Avdesh Narayan Singh, TS Kuppanna Sastri, KV Sarma, KS Shukla, Rangacharya and others have translated books, and given us various detailed studies of such works also.
Unfortunately, these remain confined to the small community of scientists who know Sanskrit.
The future
In my first essay in these series, I presented a quiz, contrasting our ignorance of Indian scientists and their contributions versus our knowledge of European scientists.
I hope some of these essays have addressed that lacuna: we know a little about Brahmagupta and Nilakantha. There was much science in the investigations of our star gazers than taught of in our philosophy.
I hope it has provoked curiosity about Indian history, especially of science and technology, and a desire to at least seek some of this information, of which we have zero exposure in the public education system.
I hope also that we as a society, try to learn about sciences of various ancient cultures, such as China, Egypt, Olmecs-Mayans, Sumeria, etc. It is fascinating that Mayans independently discovered the zero, but not the place value system, for example. And our 24-hour clock is based on Egyptian astronomy.
I am not a mathematician, an astronomer, or a historian; I don’t know Sanskrit, except for a smattering of vocabulary, especially technical and scientific. If even I can learn enough to write a series like this, what can you not do?
R Gopu delivers lectures on astronomy, history, sculpture, Sanskrit, and Tamil, and is part of the Tamil Heritage Trust. He blogs here.





