Explained: The Vedangas — Or, The Logic And Mathematics In Language

The Vedangas are six subjects created to assist in the study of the Vedas. Four of the Vedangas are about linguistics; the other two have significant mathematical sections.

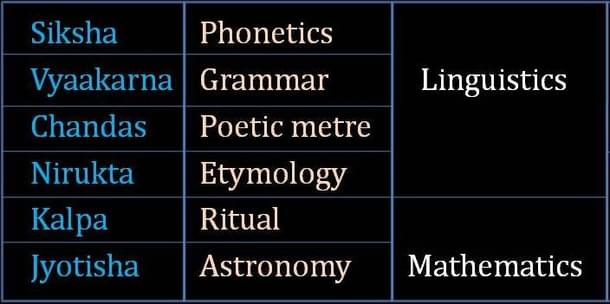
Mathematical Patterns In Akshara, Vyaakarana And Chandas

The Sanskrit alphabet is a masterpiece of analysis and organisation — and this may predate its written form. The sounds are classified as svara (vowels) and vyanjana (consonants), then grouped by origin in the mouth, voicing and aspiration.

This may seem unremarkable, until we learn a language that practically doesn’t use vowels, like Hebrew or Arabic. Pertinent to mathematics, though, is the differentiation of vowels as short (hrsva) and long (dheerga) based on the duration of pronunciation, called maatra (measure).

This is standardised in every Indian literary language, including those of the Dravidian family, but missing from European languages. Even after hearing every Indic name, city, object creatively uttered by foreigners, rarely do we appreciate this. Ah, for an Oxbridge accent!

There is a separate classification of syllables, rather than letters, as laghu (light) or guru (heavy), which is the basis of generation and classification of chandas (prosody). Each metre has a different number of syllables.

The binary nature of the syllables and the various possible combinations for letters led to the development of combinatorics: Meru-prastara, a precursor to Pascal’s triangle; and algorithms to find metrical patterns or their various aspects based on the number of syllables.

For example, consider a three-syllable metre. There are eight possible combinations of guru (G) and laghu (L) syllables.

Is this mathematics or linguistics, one might ask? Even the linguistics texts have a mathematical structure.

Sanskrit literature is in one of three forms: chandas (verse), champu (text) or sutra (brief text). All the Vedangas, composed in the Vedic era, except Jyotisha are in sutra form, in very cryptic notation, akin to modern mathematical notation.

Ironically, all the ganita siddhantas of the post-Vedic period are in chandas, poetic form. What an irony: grammar and poetry books in mathematical notation, but mathematics books in verse!

In fact, we find the oldest mentions of zero, Shunyam and Lopah, in Panini’s Ashtadhyayi (about grammar) and Pingala’s prosody, ChandaSutra, and not in the Jyotisha text!

Panini’s Ashtadhyayi

Long before Panini, Sanskrit had 11 books on grammar, by Indra, Galava, Gautama, etc. The Siva Sutra, a brilliant arrangement of letters into 14 groups, in algebraic notation, also predates Panini and was fully exploited by him.

Panini’s grammar is so algebraic in its notation, it has been an inspiration for later mathematicians, say experts. This was centuries before algebra developed. His grammar is generative rather than analytical or descriptive.

No other language in the world had such a grammar book until mathematicians developed similar notations for computer languages in the 20th century. These concepts may need a book or several lectures to explain. So they are beyond the scope of this essay.

The Sulbasutras

Egyptians and Greeks developed geometry for earth (geo) measurement (metry). We may say Indians developed vedi-metry: the Sulbasutras are manuals for configuring vedis (altars) of different shapes for performing yajnas (Vedic sacrifices).

They were measured using ropes (rajju or sulba). Baudhayana, Kaatyaayana, Apastamba, Maanava, Maitraayana, Vaaraaha and Vaadhula are seven Sulbasutras named after their composers, that survive. Their contents are very similar.

विहारयोगान्व्याख्यास्यामः । Aapastambha Sulbasutra 1.1

Vihaara-yoga-vyaakhyaasyaamaH

Translation: We make known (vyaakhyaasyaama) constructing figures (vihaara-yoga)

रज्जुसमासं वक्ष्यामः । Kaatyaayana Sulbasutra 1.1

Rajju-samaasam vakshyaaamaH

Translation: We explain (vakshyaama) by combination (samaasam) of ropes (rajju)

Unlike axiomatic Greek geometry, which is very theoretical, Sulbasutras are practical or applied. They specify rules and methods for the construction of vedi-s, finding true east, calculating areas, diagonals, choosing clay, making bricks, calculating the number of bricks, etc.

Praachi – Finding True East

समे शङ्कु निखाय
शङ्कुसम्मितया रज्जवा मण्डलं परिलिख्य
यत्र लेखयोः शङ्क्वग्रच्छाया निपतति
तत्र शङ्कू निहन्ति सा प्राची || कात्यायन शुल्बसूत्र 1–2

Translation:
Place a shanku (gnomon or a cone), on level ground,
Draw a circle with rope measuring the height of the shanku,
Where shadows fall on the circle, fix a stick (morning, evening),
That line is the praachi (line connecting the two sticks), the east-west line!

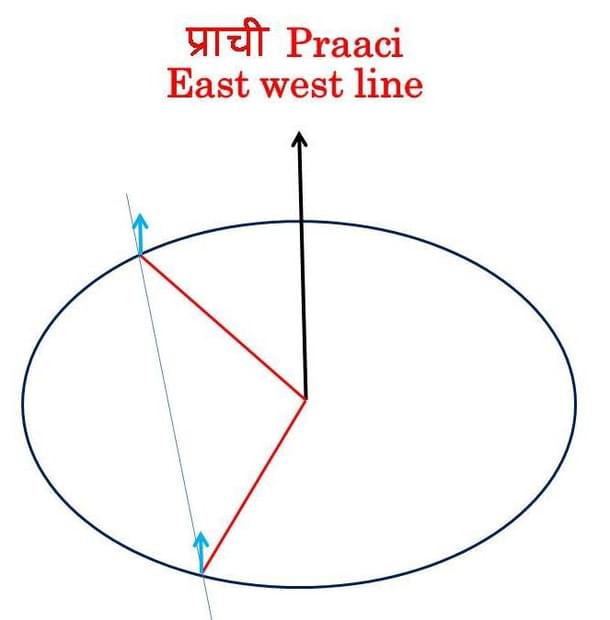
As the concept of ayana was well understood, this explains that true east is not merely the direction the sun rises, but its midpoint over the full year. The method of finding true east, using simple devices like a stick, rope, pegs is very typical of Indian astronomy.

Using The Diagonal Of A Square

चतुरश्रयाक्ष्णयारज्जुर्द्विस्तावतीं भूमीं करोति ।
समस्य द्विकरणी ॥ Aapastambha 1.5

chaturashraya akshnayaa rajju dvis-taavatim bhoomi karoti ।
samasya dvikarani ॥

Translation: The rope (rajju) on the diagonal (akshnayaa) of a square (chatur-ashra) produces (karoti) double (dvi) the area (bhumi) of the square. It equals (sama) √2 (dvikaraNi) of the side of the square.

Dvikarani literally means double-maker. To construct a square twice the size of a given square, the latter’s diagonal should be used as the side for the bigger square. The word karani can mean square root, diagonal of a square, producer, etc.

Square Root Of Two

प्रमाणं तृतीयेन वर्धयेत्तच्च चतुथेनात्मचतुस्त्रिंशोनेन सविशेषः ॥ Aapastambha 1.6

pramaaNam truteeyena vardhayet-tacca caturthena-aatma-catus-trimsha-unena sa-visheshaH ||

Translation: The measure (pramaaNam) is to be increased by its third (truteeyena) and this (aatma) again by its own fourth (caturthena) less (unena) the thirty-fourth part(catus-trimsha) approximately (sa-visheshaH).

√2 = 1 + 1/3 + 1 /3*4( 1 - 1/34 )

This is an excellent approximation; but also an indication that they didn’t understand the irrational numbers. VisheshaH means special; here the special nature is interpreted as the approximate nature of the result. A similar sutra exists for square root of three, which demonstrates the general concept.

Squaring A Circle

मण्डलं चतुरश्रं चिकीर्षन् विष्कम्भं पञ्चदशभागान्कृत्वा द्वावुद्धरेत् ।
त्रयोदशवशिष्यन्ते ।
सानित्या चतुरश्रं ॥ Apastambha 3.3 ॥

Mandalam catur-ashram cikirshan vishkambham panca-dasha-bhaagaan-krtvaa dvaar-uddharet |
trayo-dasha-avavashishyante |
sanityaa catur-ashram ||

Translation: To transform a circle (mandalam) into a square (catur-ashram), the diameter (vishkambham) is divided into 15 parts (pancha-dasha-bhaagam) and two (dvaa) of them are removed (uddharet), leaving or resulting in (avashishyante) 13 parts (trayaodasha). This gives the approximate (side of the desired) square.

This shows not only an understanding of the equation famously called ‘Pythagoras theorem’ but also an understanding that it applies not only to whole numbers.

As Baudhayaana’s is the oldest Sulbasutra containing this sutra, Fields medalist, Manjul Bhargava, as well as many other mathematicians think that the Pythagoras theorem should be renamed after Baudhaayana.

In the Classical era from Aryabhata onwards, the phrase, bhuja-koti-karna nyaaya, denoted this relationship of a hypotenuse to a right triangle, or a diagonal to a square, with bhuja, koti and karna meaning, base, perpendicular and hypotenuse, respectively.

The Sulbasutra words for these are: paarshva-maani, paryanka-maani and akshnayaa. Such a vast period of time had elapsed between the Sulbasutras and Aryabhata that even the scientific vocabulary had got transformed.

Vedanga Jyotisham

I explained some of the ideas in the Rg and Yajur Vedanga Jyotishas in the previous essay. I will touch upon some other concepts here.

One was the categorisation of some of the 27 stars into the fierce and cruel categories; this is not found in later siddhantas. A sloka referencing each star by a single letter name is another unique, unrepeated highlight.

Yet another is the use of water clocks. Pots of different sizes, called कुडव, आढक, द्रोण (kuDava, aaDhaka, drona) were used. They represented the time taken to completely drain the water in the pots (through a precise hole at the centre of the pot’s base).

Sixteen kuDava-s is an aaDhaka, 4 aaDhakas is a drona. A naadi is the time it took for 45 kuDavas of water to drain away. No explanations are given; these must have been taken from common usage. Other time measures like kala, muhurtha, parva, lagna were also introduced.

Most of the slokas in Vedanga Jyotisha are procedures for calculating various time-based phenomena. These include calculating the equinoxes, increase in the lengths of the day and night, differences between lunar and solar days, etc.

They are too complicated for this essay, so I will omit them. Remember, the purpose of the subject was explained as kaala-vidhaana-shaastram, the science of calculating time.

Another interesting point: the simple mathematical calculation of proportions called thrai-raashika, (the rule of three) is seen here. If x tasks take y units of time, how many units of time does z tasks take, is an example. Given any three of these, the fourth can be calculated.

This arithmetic, perhaps the simplest algorithm for calculating an unknown based on known quantities, which we learn in our primary schools, is as old as the Vedangas.

The astronomical phenomenon not discussed are eclipses, their calculation or prediction, celestial longitudes and latitudes, orbits of planets, etc. These subjects were studied in the subsequent era of the 18 Siddhantas.